NARASOMA NOTEBOOK

Saya mendapat tugas untuk mencari suatu persamaan yang menggambarkan lingkaran ganda :

dalam bidang bermatra dua. Satu persamaan untuk menggambarakan satu lingkaran sudah biasa, tetapi satu persamaan untuk menggambarakan lingkaran ganda, itu lain soal. Saya segera ingat, mungkin saya bisa menemukan petunjuk dalam buku geometri analitik. Saya pun membuka - buka buku kalkulus jilid tulisan Purcell dan Varberg, sembari berhara menemukan persamaan yang saya cari. Saya lalu menemukan istilah lemniskat, yang menurut buku tersebut berarti grafik dengan bentuk mirip angka delapan (setelah googling beberapa saat, pengertian itu mungkin bukan pengertian yang tepat).

Persamaan lemniskat yang diberikan dalam buku tulisan Purcell itu (dalam koordinat kutub) adalah :
Persamaan (2) adalah hasil trial and error, dari bentuknya saja langsung kelihatan kalau persamaan itu masih bisa diubah ke bentuk yang lebih sederhana. Meskipun tugas saya sudah selesai, tapi saya tertarik untuk melakukan lebih, yakni menemukan penurunannya. Setelah menghabiskan satu lembar kertas buram ukuran A4 untuk corat - coret, saya akhirnya menurunkan penurunan persamaan itu.
Mula - mula, saya menggambar lingkaran ganda itu di dalam lingkaran yang lebih besar, dengan syarat diameter masing - masing lingkaran ganda itu sama dengan jari - jari lingkaran besar yang memuatnya. Lalu saya menarik garis lurus, dari pusat lingkaran besar ke sembarang titik pada lingkaran besar, meskipun sembarang, tetapi garis ini harus membentuk sudut tertentu dengan garis mendatar (sumbu-x) agar memotong salah satu lingkaran pada lingkaran ganda. Dikandung maksud agar tali busur pada salah satu lingkaran dari lingkaran ganda itu dapat dikaitkan dengan jari - jari lingkaran besar.

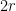
Misalkan jari - jari masing - masing lingkaran pada lingkaran ganda itu maka jari - jari lingkaran besar adalah . Panjang tali busur OP = l, dapat dihitung menggunakan rumus kosinus, yaitu :