Kenneth Krane dalam bukunya yang berjudul Modern Physics, merekomendasikan misi pencarian persamaan gerak partikel klasik sebelum menginjak persamaan Schrodiger. Ya, saya sedang mempelajarinya. Namun bagi saya pribadi, mencari persamaan gerak partikel klasik itu saja masih merupakan hal baru. Karenanya judul tulisan berikut saya awali dengan kata "belajar" agar sesuai dengan kondisi saya saat ini. Dalam hal ini saya memenggal contoh 1 bab lima buku tersebut disertai penyelesaian soal nomer 1 pada akhir bab.
Contoh 5.1
Sebuah benda bermassa 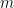 dijatuhkan dari ketinggian
dijatuhkan dari ketinggian 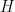 di atas sebuah tangki air. Ketika memasuki air, ia mengalami gaya apung
di atas sebuah tangki air. Ketika memasuki air, ia mengalami gaya apung 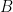 yang lebih besar dari beratnya. Gaya viskos air pada benda dapat diabaikan. Carilah perpindahan dan kecepatan benda, dihitung saat dilepaskan hingga muncul kembali ke permukaan air.
yang lebih besar dari beratnya. Gaya viskos air pada benda dapat diabaikan. Carilah perpindahan dan kecepatan benda, dihitung saat dilepaskan hingga muncul kembali ke permukaan air.
Solusi
Ambil sistem koordinat dengan 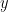 positif ke atas, dan
positif ke atas, dan 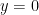 pada permukaan air. Selama benda itu jatuh bebas, ia hanya dipengaruhi oleh gaya gravitasi. Karenanya, dalam daerah udara di atas air (sebut daerah 1), dari hukum kedua Newton kita dapatkan persamaan
pada permukaan air. Selama benda itu jatuh bebas, ia hanya dipengaruhi oleh gaya gravitasi. Karenanya, dalam daerah udara di atas air (sebut daerah 1), dari hukum kedua Newton kita dapatkan persamaan
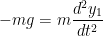
yang memiliki solusi
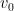
dan
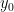
adalah kecepatan dan ketinggian awal saat
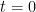
.
Saat benda memasuki air (daerah 2), gaya yang bekerja padanya menjadi
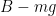
, sehingga persamaan yang didapat menjadi
dengan pemecahan
Keempat solusi memiliki empat koefisien yang belum ditentukan yakni :
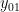
,
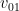
,
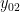
dan
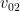
. Perhatikan bahwa
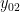
dan
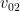
bukan nilai pada saat
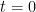
, melainkan saat meninggalkan daerah 1. Kedua koefisien pertama diperoleh dengan menerapkan syarat awal pada saaat
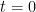
. Karena benda dilepaskan dri keadaan diam pada ketinggian tertentu, maka
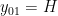
dan
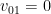
. Sehingga pemecahan di daerah 1 menjadi
Selanjutnya kita tetapkan syarat batas pada permukaan air. Misalnya
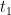
adalah saat benda memasuki air. Syarat batasnya mengharuskan fungsi
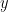
dan

bersifat kontinu di daerah perbatasan udara-air :
dan
Persyaratan pertama mengatakan bahwa benda tidak menghilang pada suatu waktu di dareah perbatasan lalu muncul kembali di tempat lain pada waktu berikutnya. Persyaratan kedua menyatakan bahwa perubahan laju benda harus mulus pada permukaan air. Jika tidak, maka
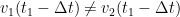
meskipun
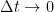
, sehingga percepatan mendekati tak hingga.Untuk menerapkan syarat batas ini, terlebih dahulu kita perlu mencari
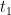
, yang diperoleh dengan mencari waktu
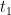
ketika
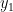
menjadi nol.
sehingga
Dengan demikian, laju benda ketika menyentuh air,
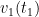
adalah
Maka syarat batas memberikan
dan
Kita pecahkan kedua persamaan ini secara serempak untuk mendapatkan
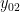
dan
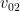
.
Sehingga pemecahan lengkap dalam daerah 2 adalah
Persamaan bagi
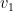
,
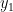
,
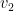
dan
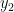
memberikan perilaku gerak benda pada saat
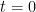
hingga ia muncul kembali ke permukaan air.
Hasil – hasil ini dapat kita terapkan untuk menghitung sifat gerak lainnya; misalnya, kita dapat mencari kedalaman maksimum yang dicapai benda, yang terjadi ketika
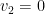
. Jika kita ambil
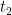
sebagai waktu pada saat ini terjadi, maka
Kedalaman
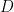
adalah nilai
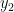
pada saat
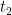
ini, yaitu
Misalkan air tersebut kita ganti dengan permukaan lantai tegar yang memantulkan benda itu secara elastik. Persamaan pada saat
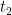
berubah drastis. Benda menerima percepatan mendekati tak hingga saat menyentuh lantai sehingga kecepatannya berubah secara diskontinu.
Berikut grafik yang menggambarkan persamaan gerak benda pada kasus pertama :
 |
| Gambar 1 : Percepatan 1 |
 |
| Gambar 2 : Kecepatan 1 |
 |
| Gambar 3 : Jarak 1 |
Dan, jika permukaan air diganti dengan lantai maka grafik akan berubah sebagai berikut :
 |
| Gambar 4 : Percepatan 2 |
 |
| Gambar 5 : Kecepatan 2 |
 |
| Gambar 6 : Jarak 2 |
Soal 1
Sebuah partikel klasik bergerak bebas dalam arah

positif
dengan laju
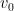
. Ketika ia melewati titik asal (
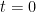
), ia memasuki daerah 1 dan mengalami perlambatan
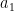
. Pada saat
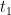
, di kedudukan
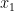
, ia meninggalkan daerah 1 dan memasuki daerah 2, serta mengalami perlambatan
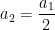
. Daerah 2 ia tinggalkan pada saat
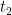
di koordinat
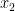
, ketika kecepatannya
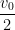
, dan kembali bergerak bebas. Tanpa menuliskan persamaan, buatlah sketsa yang memperlihatkan ketergantungan percepatan, kecepatan dan kedudukannya terhadap waktu mulai dari waktu yang lebih kecil daripada nol hingga yang lebih besar daripada
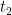
. Renungkan baik - baik apakah

,

dan

(serta kemiringan - kemiringannya) kontinu.
Penyelesaian
Pertama kita buat sketsa umum gerak partikel tersebut :
 |
| Gambar 7 : Sketsa umum gerak partikel dalam soal 1 |
Perhatikan, di sini kita pilih sistem koordinat dengan nilai positif ke atas yang menyatakan pertambahan jarak sedangkan arahnya diabaikan. Karena itu, secara otomatis "perlambatan" bertempat di bawah di bawah sumbu horizontal
.
 |
| Gambar 8 : Percepatan 3 |
Grafik kecepatan diberikan oleh sketsa berikut
 |
| Gambar 9 : Kecepatan 3 |
Terdapat suatu titik di mana perhitungan jarak dimulai (
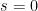
), saat itu
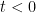
.
 |
| Gambar 10 : Jarak 3 |
|
Di sini terlihat bahwa perubahan kecepatan dan kedudukan partikel tersebut kontinu, sedangkan percepatannya tidak.

















