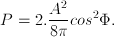|
| Albert Einstein |
TENTANG ELEKTRONDINAMIKA BENDA - BENDA BERGERAK
Oleh A. Einstein
30 Juni 1905
Oleh A. Einstein
30 Juni 1905
Telah diketahui bahwa elektrodinamika Maxwell-seperti yang biasa dipahami saat ini, jika diterapkan pada benda bergerak, akan mengarah pada asimetri gejala yang tidak tampak pada fenomena. Ambil contoh, kebalikan aksi elektrodinamik dari gerak magnet dan konduktor. Fenomena yang diamati di sini hanya bergantung pada gerak relatif dari konduktor dan magnet, sedangkan penampakan yang biasa mengacu pada perbedaan tajam antara dua kasus di mana salah satu dari benda - benda ini bergerak. Karena jika magnet bergerak dan konduktor diam, muncul sebuah lingkungan medan magnet dan listrik dengan energi tertentu, yang menghasilkan arus tepat di mana konduktor berada. Tetapi jika magnet diam dan konduktor yang bergerak, tidak ada medan listrik timbul di lingkungan magnet. Dalam konduktor, kita temukan gaya gerak listrik, yang secara otomatis tidak ada energi terkait, namun yang menimbulkan-dengan asumsi kesamaan gerak relatif dalam dua kasus yang dibahas- arus listrik lintasan yang sama dan intensitas yang sama seperti yang diproduksi oleh gaya listrik dalam kasus sebelumnya.
Beberapa contoh semacam ini, bersamaan dengan usaha yang gagal untuk menemukan setiap gerak bumi relatif terhadap "medium cahaya," menunjukkan bahwa fenomena elektrodinamik maupun mekanik tidak memiliki sifat yang terkait dengan ide diam mutlak. Saran mereka lebih karena, seperti yang telah ditunjukkan pada orde pertama besaran kecil, hukum elektrodinamika dan optik akan sah untuk semua kerangka acuan di mana persamaan mekanika tetap berlaku.[1] Kami akan meningkatkan dugaan ini ( yang selanjutnya akan disebut sebagai "Prinsip Relativitas") ke status postulat, dan kami juga akan memperkenalkan postulat lain, yang sekilas tampak tak bersesuaian dengan, postulat sebelumnya, yaitu cahaya yang selalu bergerak dalam ruang hampa dengan laju tetap c yang tidak tergantung dari keadaan gerak sumber. Keduanya cukup untuk menunjang pencapaian sebuah teori yang sederhana dan konsisten tentang elektrodinamika benda bergerak berdasarkan teori Maxwell untuk benda diam. Pengenalan terhadap "eter transparan"akan terbukti menjadi demikian berlebihan karena pandangan yang dikembangkan di sini tidak memerlukan adanya "ruang diam mutlak" dengan sifat khusus, ataupun menetapkan sebuah vektor kecepatan ke sebuah titik dalam ruang kosong dimana proses elektromagnetik berlangsung.
Teori yang dikembangkan di sini didasarkan - seperti semua elektrodinamika- pada gerak benda tegar, karena pernyataan - pernyataan yang berasal dari semua teori tersebut harus berkaitan dengan hubungan antara benda tegar (sistem koordinat), jam, dan gejala - gejala elektromagnetik. Kurangnya pertimbangan terhadap keadaan ini beasaskan pada kesulitan - kesulitan yang terdapat pada elektrodinamika benda bergerak yang dipahami saat ini.
I. BAGIAN KINEMATIKA
§ 1. Definisi kejadian serentak (simultaneity)
Mari kita mengambil sistem koordinat di dimana persamaan mekanika Newton berlaku dengan baik.[2] Untuk membuat presentasi kita lebih tepat dan untuk membedakan sistem koordinat secara verbal dari yang lain yang akan diperkenalkan selanjutnya, kami menyebutnya "sistem stasioner."
Jika sebuah titik materi berada dalam keadaan diam relatif terhadap sistem koordinat ini, posisinya dapat ditentukan secara relatif oleh pengukuran menggunakan standar-ukur tegar dan metode geometri Euclidean, serta dapat dinyatakan dalam koordinat Kartesius.
Jika kita ingin melukiskan gerak titik materi tersebut, kita berikan nilai - nilai koordinat-nya sebagai fungsi waktu. Sekarang kita harus mencatat dengan seksama dalam pikiran bahwa gambaran matematis semacam ini tidak memiliki arti fisik kecuali kita cukup mengerti dengan jelas tentang apa yang kita pahami sebagai "waktu". Kita harus mempertimbangkan bahwa semua penilaian kita di mana waktu yang memegang peranan adalah "waktu." yang selalu menjadi obyek penentu dari peristiwa simultan. Jika misalnya saya berkata, "Kereta itu sampai itu di sini di pukul 07:00 tepat," maka yang saya maksud adalah seperti ini: "Jarum jam tangan saya menunjuk angka 7 dan kedatangan kereta itu adalah kejadian simultan."[3]
Tampaknya mungkin untuk mengatasi semua kesulitan terkait definisi "waktu" dengan menggantikan "arloji kecil di tangan saya" untuk "waktu". Sebenarnya definisi ini bisa memuaskan jika dan hanya jika kita mendefinisikan waktu secara eksklusif untuk sebuah tempat dimana jam tangan berada, tetapi ia tidak lagi memuaskan ketika kita harus terhubung dengan serangkaian waktu dari peristiwa - peristiwa yang terjadi di tempat berbeda, atau -apa yang mengacu pada kejadian serupa- untuk meninjau waktu sebuah peristiwa yang terjadi di tempat yang jauh dari arloji.
Tampaknya mungkin untuk mengatasi semua kesulitan terkait definisi "waktu" dengan menggantikan "arloji kecil di tangan saya" untuk "waktu". Sebenarnya definisi ini bisa memuaskan jika dan hanya jika kita mendefinisikan waktu secara eksklusif untuk sebuah tempat dimana jam tangan berada, tetapi ia tidak lagi memuaskan ketika kita harus terhubung dengan serangkaian waktu dari peristiwa - peristiwa yang terjadi di tempat berbeda, atau -apa yang mengacu pada kejadian serupa- untuk meninjau waktu sebuah peristiwa yang terjadi di tempat yang jauh dari arloji.
Kita mungkin, tentu saja, membatasi diri kita dengan nilai waktu yang ditentukan oleh pengamat ditempatkan bersama dengan jam tangan pada titik pusat-koordinat, dan mengkoordinasi posisi yang berkaitan antara jam tangan dengan sinyal cahaya, yang diberikan oleh setiap peristiwa untuk diukur waktunya, dan sampai padanya melalui ruang hampa. Namun koordinasi ini memiliki kekurangan yang tidak bebas dari sudut pandang pengamat (dengan arlojinya), seperti yang kita tahu dari pengalaman. Kami sampai pada sebuah ketetapan yang jauh lebih praktis sepanjang pola pikir berikut ini.
Jika pada titik A dalam ruang ada sebuah jam, seorang pengamat pada A dapat menentukan nilai waktu sebuah kejadian yang cukup dekat dengan A, dengan mencari posisi jarum jam tangan mana yang bersamaan dengan peristiwa tersebut. Dan jika ada di titik B dalam ruang dengan jam lain yang identik dengan A, maka sangat mungkin bagi pengamat di B untuk menentukan waktu kejadian di lingkungan dekat B. Tapi tanpa asumsi lebih lanjut tidak mungkin untuk membandingkan, dalam hal waktu, kejadian di A dengan kejadian di B. Kami telah membuat definisi yang jauh tentang " waktu A" dan"waktu B". Tetapi kami belum mendefinisikan "waktu" yang berlaku umum untuk A dan B, untuk yang terakhir tidak dapat didefinisikan seluruhnya kecuali kita menetapkan suatu definisi bahwa "waktu" yang dibutuhkan oleh cahaya untuk bergerak dari A ke B sama dengan "waktu" itu diperlukannya dari B ke A. Ambil contoh sebuah sinar cahaya berawal pada " waktu A" tA bergerak dari A ke B, dan misalkan pada "waktu B " tB dipantulkan di B dalam arah A, kemudian tiba lagi di A pada "waktu A" t'A.
Kita asumsikan bahwa definisi singkronisme ini bebas dari kontradiksi, dan mungkin untuk setiap nilai titik ; dan bahwa relasi berikut adalah sah secara universal :
- Jika jam di B singkron dengan jam di A, maka sebaliknya jam di A singkron dengan jam di B.
- Jika jam di A singkron dengan jam di B, begitu juga dengan jam di C, maka jam di B dan C saling singkron.
Dengan bantuan percobaan fisika dalam angan - angan tersebut kita telah menyelesaikan apa yang dipahami sebagai jam singkron-diam yang terletak di tempat berbeda, juga mendapatkan definisi "keserempakan" atau "kesingkronan", maupun "waktu". "Waktu" dari sebuah kejadian adalah suatu kondisi dimana terjadi keserempakan antara peristiwa tersebut dengan jam stasioner yang terletak di tempat kejadian, jam ini dikatakan singkron, dan tentunya akan singkron untuk semua penentuan waktu dengan jam stasioner yang khusus.
Dalam kaitannya dengan pegalaman, lebih lanjut kita asumsikan persamaan :
sebagai konstanta universal-kecepatan cahaya di ruang hampa.
Merupakan suatu hal yang penting untuk mendefinisikan waktu dalam arti jam yang diam dalam sistem stasioner, dan sang waktu kini telah dijamin sesuai dengan sistem stasioner yang kita sebut "waktu stasioner".
§ 2. Tentang Relativitas Panjang dan Waktu
Ide ini didasarkan pada prinsip relativitas dan prinsip kekonstanan kecepatan cahaya. Kami mendefinisikan keduanya sebagai berikut :
Hukum - hukum yang menyatakan berubahnya sistem fisik adalah tidak terpengaruh, jika perubahan kadaan ini mengacu pada satu sama lain di antara dua sistem koordinat dalam gerak lurus seragam.
Setiap sinar cahaya yang bergerak dalam sistem koordinat "stasioner" dengan kecepatan tertentu c. Tidak peduli apakah sinar itu dipancarkan oleh benda diam maupun bergerak. Karenanya :
dimana interval waktu di sini seperti yang telah dijelaskan dalam § 1.
Misalnya diberikan sebuah batang tegar yang diam, dan panjangnya sebesar l yang diukur menggunakan alat ukur yang diam juga. Sekarang kita bayangkan sumbu batang terletak di sepanjang sumbu-x dari suatu sistem koordinat stasioner, serta ia bergerak translasi paralel secara seragam dengan kecepatan υ sepanjang sumbu-x positif. Sekarang kita cari tahu panjang batang bergerak ini, dan bayangkan panjangnya dipastika oleh dua operasi berikut :
- Pengamat bergerak bersamaan dengan pengukur yang telah diberikan dan batang yang akan diukur, lalu ia mengukur panjang batang secara langsung dengan cara menghimpitkan alat ukur itu di atasnya. Seperti jika ketiganya dalam keadaan diam.
- Dengan menggunakan jam stasioner yang tlah diatur dalam sistem stasioner serta telah dicocokkan menurut definisi § 1, pengamat memastikan, di titik mana (dalam sistem stasioner) kedua ujung batang yang diukur itu berada pada saat tertentu. Jarak antara kedua titik itu diukur menggunakan alat ukur tadi, dimana pada kasus ini diam, yang bias dikatakan sebagai "panjang batang".
Dalam penyesuaiannya dengan prinsip relativitas, panjang yang diukur dengan metode (a)-selanjutnya kami sebut "panjang batang dalam sistem yang bergerak"- harus sama dengan panjang l dari batang-diam.
Panjang yang diukur menggunakan metode (b) akan kami sebut "panjang benda bergerak dalam sistem stasioner". Dengan begini kita dapat menentukan panjang batang berdasarkan kedua prinsip di atas, dan kita akan temukan bahwa panjang ini berbeda dengan l.
Kinematika saat ini mengasumsikan bahwa panjang yang diukur oleh kedua metode adalah tepat sama, atau dengan kata lain, batang tegar yang bergerak tersebut pada waktu t, boleh jadi, dalam sudut pandang geometri digambarkan oleh benda yang sama dalam posisi tertentu.
Lebih jauh kita bayangkan bahwa kedua ujung batang A dan B, dipasang jam - jam yang singkron dengan sebuah jam yang berada dalam sistem stasioner, sehingga dapat dikatakan bahwa waktu yang ditunjukkan oleh jam tersebut sesuai dengan "waktu dalam sistem stasioner" di tempat masing - masing. Jam - jam tersebut "singkron terhadap sistem stasioner".
Selanjutnya kita bayangkan bahwa untuk setiap jam terdapat seorang pengamat yang bergerak, dan pengamat - pengamat tersebut menggunakan kedua jamnya sesuai ketentuan yang telah ditetapkan dalam § 1 untuk singkronisasi kedua jam. Misalkan sebuah sinar cahaya berangkat dari A pada waktu[4] tA, dan dipantulkan di B pada saat tB, lalu mencapai A lagi pada saat t'A. Mempertimbangkan prinsip kekonstanan kecepatan cahaya, kita dapatkan :
dimana rAB menunjukkan panjang batang bergerak -yang diukur dalam sistem stasioner. Para pengamat bergerak bersama dengan batang, dengan demikian mereka akan menemukan bahwa kedua jam tidak singkron lagi, sementara para pengamat yang berada dalam sistem stasioner akan menyatakan bahwa jam - jam mereka singkron.
Jadi kita telah mengetahui bahwa kita tidak dapat mencantumkan sifat mutlak untuk konsep kejadian serentak, akan tetapi kedua kejadian tersebut , yang mana terlihat serempak dari sebuah sistem koordinat, bisa saja tidak serentak jika dipandang dari sebuah sistem koordinat yang bergerak relatif terhadap sistem tersebut.
§ 3. Teori Transformasi Koordinat dan Waktu dari Sistem Stasioner ke Sistem Lain dalam Gerak Seragam Relatif Terhadap Sistem yang Pertama
Misalkan kita yang sedang berada dalam ruang "stasioner" mengambil dua sistem koordonat, yakni dua buah sistem, masing - masing terdiri dari tiga garis tegar yang saling tegak lurus satu sama lainnya serta berasal dari satu titik pusat. Andaikan sumbu X dari kedua sistem berimpit, sumbu Y dan Z milik keduanya masing - masing sejajar. Andaikan dalam setiap sistem disediakan batang-pengukur tegar dan sebuah jam, serta misalakan kedua alat ukur dan jam - jam dari kedua sistem itu dalam semua ukuran adalah sama.
Sekarang, misalkan titik asal milik salah satu sistem (k) bergerak dengan kecepatan konstan υ dalam arah x positif terhadap sistem stasioner (K). Kecepatan ini terhubung ke sumbu - sumbu koordinat, batang pengukur yang bersangkutan serta jam - jam tadi. Terhadap sebarang waktu dalam sistem stasioner K selanjutnya akan terkait dengan posisi tertentu dari setiap sumbu sistem yang bergerak tadi, dan berdasarkan alasan simetri kita dapat mengasumsikan bahwa gerak sistem k sedemikian sehingga sumbu - sumbu sistem pada saat t (lambang "t" selalu menyatakan waktu milik sistem stasioner) adalah sejajar terhadap sumbu - sumbu sistem stasioner.
Sekarang kita bayangkan ruang yang hendak diukur dari sistem stasioner K menggunakan batang pengukur stasioner, dan juga dari sistem bergerak k menggunaan pengukur yang bergerak bersamaan dengannya; dengan demikian kita dapatkan koordinat - koordinat x, y, z, dan ξ, η, ζ. Lebih lanjut, kita misalkan waktu t dalam sistem stasioner ditentukan untuk semua titik di mana jam - jam itu berada menggunakan sinyal cahaya sesuai metode yang telah ditunjukkan dalam § 1; demikian pula misalkan waktu sistem bergerak τ ditentukan untuk setiap titik dari sistem itu dimana jam berada, diam relatif terhadap sistem bergerak, dengan menggunakan metode yang diberikan dalam § 1 yakni sinyal cahaya.
Untuk sebarang nilai sistem x, y, z, t, yang mana secara lengkap mendefinisikan tempat dan waktu terjadinya beuah peristiwa dalam sistem stasioner, terdapat pula nilai sistem ξ, η, ζ, τ yang menentukan kejadian relatif terhadap sistem k. Tugas kita sekarang adalah menemukan persamaan yang menghubungkan besaran - besaran itu.
Awalnya telah jelas bahwa persamaan tersebut haruslah linier berdasarkan pertimbangan terhadap sifat homogen yang kita berikan pada ruang dan waktu.
Jika kita memilih x‘ = x - υt, maka jelas bahwa titik - titik yang diam relatif terhadap sistem k harus mempunyai nilai sistem x‘, y, z yang tidak terikat oleh waktu. pertama, kita definisikan τ sebagai fungsi x‘, y, z, dan t. Untuk melakukan ini kita harus menyatakan dalam persamaan, bahwa τ tak lain daripada ringkasandata jam yang diam relatif terhadap sistem k, yang mana jam - jam itu telah dicocokkan menurut aturan § 1.
Misalkan dari titik asal sistem k dipancarkan seberkas sinar pada saat τ0 sepanjang sumbu X ke x', dan pada waktu τ1 dipantulkan kembali ke titik asal sehingga sinar itu tiba pada waktu τ2; maka kita punya 1/2(τ0+τ2) = τ1, atau, dengan menyisipkan argumen - argumen fungsi τ dan menerapkan prinsip kekonstanan kecepatan cahaya dalam ruang hampa :
Karena itu, jika x’ dipilih nilai yang sangat kecil mendekati nol,
atau
Perlu dicatat bahwa alih - alih sebagai pusat koordinat kita dapat memilih sebarang titik lain untuk titik asal sinar, dan persamaan yang diperoleh adalah sah untuk semua nilai x‘, y, z.
Pertimbangan analogis - yang diterapkan pada sumbu Y dan Z- yang terpikirkan adalah cahaya selalu bergerak tersebar sepanjang sumbu - sumbu itu, ketika dilihat dari sistem stasioner, dengan kecepatan  memberikan
memberikan
 memberikan
memberikanKarena τ merupakan fungsi linier, dari persamaan - persamaan ini diperoleh :
dimana a merupakan fungsi Φ(υ) yang saat ini masih belum diketahui, dan untuk singkatnya diasumsikan bahwa di titik asal k, τ = 0, jika t = 0.
Dengan bantuan hasil ini, dengan mudah kita dapat menentukan besaran - besaran ξ, η, ζ dengan menyatakan dalam persamaan bahwa cahaya (seperti yang dibutuhkan oleh prinsip kekonstanan kecepatan cahaya yang dikombinasikan dengan prinsip relativitas) selalu tersebar dengan kecepatan c ketika diukur dalam sistem yang bergerak. Untuk sebuah sinar yang dipancarkan pada saat τ = 0 dalam arah ξ positif.
Tetapi sinar itu bergerak relatif terhadap titik awal k, yang ketika diukur dalam sistem stasioner dengan kecepatan c-υ, sehingga
Jika kita menyisipkan nilai t ke dalam persamaan untuk ξ, kita dapatkan
Secara analog kita temukan, dengan mempertimbangkan sinar bergerak sepanjang kedua sumbu lain, maka
jika
Dengan demikian
Subtitusikan nilai x’, diperoleh
dimana
dan Φ merupakan fungsi υ yang masih belum diketahui. Jika tidak ada asumsi apapun yang dibuat untuk titik awal sistem bergerak dan titik nol untuk τ, maka sebuah konstanta tambahan harus diletakkan pada setiap sisi kanan persamaan - persamaan itu.
Sekarang kita dapat membuktikan bahwa sebarang sinar cahaya, yang diukur dalam sistem bergerak, adalah tersebar dengan kecepatan c. Jika, seperti yang telah diasumsikan bahwa ini adalah kasus dalam sistem stasioner; kita belum dilengkapi dengan pembuktian bahwa prinsip kekonstanan kecepatan cahaya berkesesuaian dengan prinsip relativitas.
Pada saat t = τ = 0, ketika titik asal koordinat kedua sistem masih berimpit, misalkan ada gelombang sferis (berbentuk bola) dipancarkan darinya, dan tersebar dengan kecepatan c dalam sistem K. Jika (x, y, z) merupakan titik yang dicapai oleh gelombang ini, maka
Transformasikan persamaan ini dengan bantuan persamaan trasnformasi di atas, dan setelah melakukan perhitungan sederhana kita dapatkan :
Gelombang yang berada dalam pertimbangan kita tak lain adalah gelombang sferis dengan kecepatan sebar c ketika ditinjau dari sistem bergerak. Hal ini menunjukkan bahwa kedua prinsip fundamental kita selaras.[5]
Dalam persamaan transformasi yang telah dikembangkan terdapat sebuah fungsi Φ(υ) yang belum diketahui, dimana akan kita tentukan sekarang.
Untuk tujuan ini kita perknalkan sistem koordinat ketiga K', relatif terhadap sistem k dalam gerak seragam sejajar sumbu Ξ,[*1] sedemikian sehingga titik asal koordinat dari sistem K', bergerak dengan kecepatan -υ dalam sumbu Ξ. Pada saat t = 0, kita misalkan ketiga titik asal kordinat - korodinat itu berimpit, dan ketika t = x = y = z = 0 waktu t' untuk sistem K' juga nol. Kita sebut koordinat - koordinat yang diukur dalam sistem K', x, y, z, dan dengan penerapan ganda dari peramaan transformasi kita sebelumnya didapatkan :
Karena relasi antara x‘, y‘, z‘ dan x, y, z tidak memuat waktu t, sistem K dan K' adalah diam relatif satu sama lain, dan telah jelas juga bahwasanya transformasi dari K ke K' haruslah identik. Dengan demikian
Karena relasi antara x‘, y‘, z‘ dan x, y, z tidak memuat waktu t, sistem K dan K' adalah diam relatif satu sama lain, dan telah jelas juga bahwasanya transformasi dari K ke K' haruslah identik. Dengan demikian
Φ(υ)Φ(-υ) = 1
Sekarang kita selidiki arti dari Φ(υ). Kita pusatkan perhatian kita pada sumbu Y dari sistem k yang terletak di antara ξ = 0, η = 0, ζ = 0 dan ξ = 0, η = l, ζ = 0. Bagian sumbu Y ini merupakan batang bergerak tegak lurus terhadap sumbunya dengan kecepatan υ relatif terhadap sistem K. Titik ujung dalam koordinat K
dan
Panjang batang yang terukur di K adalah l / Φ(υ); dan ini memberikan kita arti fungsi Φ(υ). Berdasarkan alasan simetri, kini jelas bahwa panjang batang yang bergerak tegak lurus terhadap sumbunya, yang diukur dalam sistem stasioner, harus bergantung pada kecepatan saja dan tidak pada arah maupun cara gerak. Panjang batang bergerak itu jika diukur dalam sistem stasioner tidak berubah, karena itu, jika υ dan -υ dipertukarkan maka akan diikuti oleh l / Φ(υ) = l / Φ(-υ), atau
Φ(υ) = Φ(-υ).
Dari relasi ini dan yang sebelumnya ditemukan Φ(υ) = 1, sehingga persamaan - persamaan transformasi yang telah ditemukan akan berbentuk
dimana
§ 4. Arti Fisis Persamaan - Persamaan yang Diperoleh dalam Kaitannya dengan Benda Tegar dan Jam yang Bergerak
Kita bayangkan sebuah bola tegar[6] dengan jari - jari R, yang diam relatif terhadap sistem k, dan pusatnya terletak di pusat k. Persamaan permukaan bola yang bergerak relatif terhadap sistem K dengan kecepatan υ adalah
Persamaan permukaan ini jika dinyatakan dalam x, y, z pada waktu t = 0 adalah
Sebuah benda tegar yang diukur dalam keadaan diam berbentuk bola, jika berada dalam keadaan bergerak -dipandang dari sistem stasioner- akan berbentuk elipsoid yang berputar terhadap sumbu
Dimensi Y dan Z dari lingkaran (begitu juga setiap benda tegar apapun bentuknya) tidak tampak berubah karena gerakan, sedangkan dimensi X nampak memendek dengan perbandingan  yakni bahwa nilai terbesar υ mengakibatkan pemendekan maksimal. Untuk υ = c semua benda bergerak -dilihat dari sistem "stasioner"- akan berkontraksi hingga nampak seperti bidang datar.[*2] Untuk nilai kecepatan yang lebih besar dari cahaya pembahasan kita menjadi tidak berguna; kita akan, bagaimanapun juga, kita akan menemukan bahwa kecepatan cahaya dalam teori kami secara fisik telah mewakili kecepatan tak hingga.
yakni bahwa nilai terbesar υ mengakibatkan pemendekan maksimal. Untuk υ = c semua benda bergerak -dilihat dari sistem "stasioner"- akan berkontraksi hingga nampak seperti bidang datar.[*2] Untuk nilai kecepatan yang lebih besar dari cahaya pembahasan kita menjadi tidak berguna; kita akan, bagaimanapun juga, kita akan menemukan bahwa kecepatan cahaya dalam teori kami secara fisik telah mewakili kecepatan tak hingga.
 yakni bahwa nilai terbesar υ mengakibatkan pemendekan maksimal. Untuk υ = c semua benda bergerak -dilihat dari sistem "stasioner"- akan berkontraksi hingga nampak seperti bidang datar.[*2] Untuk nilai kecepatan yang lebih besar dari cahaya pembahasan kita menjadi tidak berguna; kita akan, bagaimanapun juga, kita akan menemukan bahwa kecepatan cahaya dalam teori kami secara fisik telah mewakili kecepatan tak hingga.
yakni bahwa nilai terbesar υ mengakibatkan pemendekan maksimal. Untuk υ = c semua benda bergerak -dilihat dari sistem "stasioner"- akan berkontraksi hingga nampak seperti bidang datar.[*2] Untuk nilai kecepatan yang lebih besar dari cahaya pembahasan kita menjadi tidak berguna; kita akan, bagaimanapun juga, kita akan menemukan bahwa kecepatan cahaya dalam teori kami secara fisik telah mewakili kecepatan tak hingga. Telah jelas bahwa hasil yang sama berlaku pada benda - benda diam dalam sistem "stasioner", jika dilihat dari sebuah sistem yang bergerak seragam.
Lebih lanjut, kita bayangkan salah satu jam yang telah memenuhi syarat untuk menunjukkan waktu t relatif terhadap sistem stasioner, dan waktu τ ketika diam relatif terhadap sistem bergerak, yang diletakkan di titik asal koordinat k, yang juga disesuaikan dengan penandaan waktu τ. Berapakah nilai waktu jam ini, ketika diukur dari sistem stasioner?
Di antara besaran - besaran x, t dan τ yang menunjukkan posisi jam, terbukti kita punya x = υt dan
Dengan demikian,
yang diikuti oleh fakta bahwa waktu yang ditandai oleh jam (jika dilihat dari sistem stasioner) akan melambat sebanyak  detik per detik, atau -dengan mengabaikan besaran (magnitude) orde empat dan yang lebih tinggi- sebesar
detik per detik, atau -dengan mengabaikan besaran (magnitude) orde empat dan yang lebih tinggi- sebesar  .
.
 detik per detik, atau -dengan mengabaikan besaran (magnitude) orde empat dan yang lebih tinggi- sebesar
detik per detik, atau -dengan mengabaikan besaran (magnitude) orde empat dan yang lebih tinggi- sebesar  .
.Dari sini, selanjutnya akan terjadi konsekuensi aneh. Jika di titik A dan B dari sistem K terdapat jam stasioner yang ditinjau dari sistem stasioner adalah singkron; dan jika jam di A bergerak dengan kecepatan υ sepanjang garis AB ke B, maka ketika ia tiba di B kedua jam tidak lagi singkron, tetapi jam yang bergerak dari A ke B tertinggal oleh jam satunya yang terletak di B sebanyak  (sampai besaran orde empat dan yang lebih tinggi), t menjadi waktu yang dibutuhkan untuk menempuh perjalanan dari A ke B.
(sampai besaran orde empat dan yang lebih tinggi), t menjadi waktu yang dibutuhkan untuk menempuh perjalanan dari A ke B.
 (sampai besaran orde empat dan yang lebih tinggi), t menjadi waktu yang dibutuhkan untuk menempuh perjalanan dari A ke B.
(sampai besaran orde empat dan yang lebih tinggi), t menjadi waktu yang dibutuhkan untuk menempuh perjalanan dari A ke B. Jelas hasil ini masih berlaku jika jam itu bergerak dari A ke B dalam sebarang garis poligon, dan juga ketika titik A dan B berimpit.
Jika kita mengasumsikan bahwa hasil yang terbukti sah untuk garis poligon itu juga sah untuk garis yang melengkung secara kontinu, kita tiba pada hasil ini : Jika salah satu dari dua jam singkron di A digerakkan dalam kurva tertutup dengan kecepatan konstan relatif terhadap A, dan perjalanan itu memakan waktu t detik, dibanding dengan jam yang tertinggal di A pada saat kedatangannya jam bergerak itu akan  detik lebih lambat. Berdasarkan hal itu kita simpulkan bahwa keseimbangan jam[7] di daerah khatulistiwa harus lebih lambat, dengan nilai yang sangat kecil, daripada jam identik yang ditempatkan di salah satu kutub dalam kondisi yang sama.
detik lebih lambat. Berdasarkan hal itu kita simpulkan bahwa keseimbangan jam[7] di daerah khatulistiwa harus lebih lambat, dengan nilai yang sangat kecil, daripada jam identik yang ditempatkan di salah satu kutub dalam kondisi yang sama.
 detik lebih lambat. Berdasarkan hal itu kita simpulkan bahwa keseimbangan jam[7] di daerah khatulistiwa harus lebih lambat, dengan nilai yang sangat kecil, daripada jam identik yang ditempatkan di salah satu kutub dalam kondisi yang sama.
detik lebih lambat. Berdasarkan hal itu kita simpulkan bahwa keseimbangan jam[7] di daerah khatulistiwa harus lebih lambat, dengan nilai yang sangat kecil, daripada jam identik yang ditempatkan di salah satu kutub dalam kondisi yang sama. § 5. Komposisi Kecepatan
Dalam sistem k yang bergerak sepanjang sumbu X relatif terhadapK dengan kecepatan υ, misalkan terdapat sebuah titik yang bergerak sesuai persamaan
Dibutuhkan : gerak titik relatif terhadap sistem K. Jika dengan bantuan persamaan transformasi yang dikembangkan dalam § 3 dan memasukkan nilai - nilai x, y, z, t ke dalam persamaan gerak titik itu, maka kita dapatkan
Dengan demikian hukum jajargenjang kecepatan (parallelogram of velocities) akan sah menurut teori kami hanya untuk pendekatan pertama. Kita atur[*3]
a merupakan sudut yang dibentuk oleh vektor kecepatan υ dan w. Dan setelah perhitungan sederhana kita dapatkan[*4]
Pantas diucapkan bahwa υ dan w termasuk dalam pengungkapan kecepatan resultan secara simetris. Jika w juga mempunyai arah sepanjang sumbu X, kita dapatkan
Pernyataan ini menimbulkan kenyataan bahwa penjumlahan dua nilai kecepatan yang lebih kecil dari c, akan selalu menghasilkan kecepatan total yang juga kurang dari c. Karna itu jika kita menyusun υ = c – κ, w = c - λ, κ dan λ bernilai positif serta kurang dari c, maka
Lebih lanjut, hal ini juga didikuti oleh fakta bahwa kecepatan cahaya tidak berubah oleh penjumlahannya dengan kecepatan lain yang lebih kecil dari kecepatan cahaya. Untuk kasus ini kita dapatkan
Bisa juga kita dapatkan rumus V, untuk kasus dimana υ dan w searah, dengan menjumlahkan kedua transformasi menurut aturan § 3. Jika dalam penjumlahan sistem K dan k yang dimodelkan dalam § 3 kita tetap menggunakan sistem koordinat lain k' yang bergerak sejajar terhadap k, titik asal-nya bergerak sepanjang sumbu Ξ[*5] dengan kecepatan w, kita dapatkan persamaan - persamaan dengan besaran x, y, z, t dan besaran yang terkait dengan k', yang mana perbedaannya dengan persamaan dalam § 3 hanya pada penempatan υ yang mengambil nilai
dari sini kita lihat bahwa transformasi paralel seperti itu -tentu saja- membentuk suatu grup.
Sekarang kita telah menyimpulkan hukum - hukum yang diperlukan oleh kinematika dalaam kaitannya dengan kedua prinsip kita, dan akan kita lanjutkan untuk menjelaskan penggunaannya dalam elektrodinamika.
II. BAGIAN ELEKTRODINAMIKA
§ 6. Transformasi Persamaan Maxwell-Hertz untuk Ruang Hampa. Tentang Sifat Gaya Gerak Listrik yang Terdapat dalam Medan Magnet Selama Gerakan Berlangsung
Misalkan persamaan - persamaan Maxwell-Hertz untuk ruang hampa berlaku dalam sistem stasioner K, maka kita punya
dimana (X,Y,Z) menyatakan vektor gaya listrik, dan (L,M,N) menyatakan gaya magnet. Jika kita menerapkan persamaan - persamaan tersebut ke dalam transformasi yang telah diterangkan dalam § 3, dengan mengacu proses elektromagnetik pada sistem koordinat tersebut, yang bergerak dengan kecepatan υ, kita dapatkan persamaan - persamaan
dimana
Sekarang, prinsip relativitas dibutuhkan jika persamaan Maxwell-Hertz untuk ruang hampa berlaku dalam sistem K, maka persamaan - persamaan itu juga berlaku dalam sistem k; artinya vektor listrik dan magnet -(X', Y', Z') dan (L', M', N')- dalam sistem bergerak k, yang didefinisikan oleh efek gaya geraknya terhadap resistansi elektrik maupun magnetik, memenuhi persamaan berikut :
Ternyata kedua sistem persamaan yang didapatkan untuk sistem k harus menyatakan hal yang sama, karena kedua sistem persamaan itu ekuivalen dengan persamaan Maxwell-Hertz untuk sistem K. Oleh karenanya, lebih lanjut, persamaan - persamaan dari kedua sistem sesuai, dengan pengecualian simbol - simbol bagi vektor, maka diperoleh fakta bahwa fungsi yang terdapat dalam sistem pesamaan itu di tempat yang bersesuaian harus cocok kecuali untuk faktor  yang sama untuksemua fungsi sistem persamaan. Ia juga terbebas dari ξ, η, ζ, dan τ tetapi bergantung pada υ. Dan kita akan mempunyai hubungan
yang sama untuksemua fungsi sistem persamaan. Ia juga terbebas dari ξ, η, ζ, dan τ tetapi bergantung pada υ. Dan kita akan mempunyai hubungan
 yang sama untuksemua fungsi sistem persamaan. Ia juga terbebas dari ξ, η, ζ, dan τ tetapi bergantung pada υ. Dan kita akan mempunyai hubungan
yang sama untuksemua fungsi sistem persamaan. Ia juga terbebas dari ξ, η, ζ, dan τ tetapi bergantung pada υ. Dan kita akan mempunyai hubungan Jika sekarang kita balik sistem persamaan ini, pertama dengan menyelesaikan persamaan yang baru diperoleh, dan kedua dengan menerapkan persamaan - persamaan itu pada transformasi balik (dari k ke K) yang ditandai oleh kecepatan -υ, berikutnya ketika kita pertimbangkan kedua sistem persamaan sehingga persamaan yang kita peroleh harus identik, yaitu  Karena itu, berdasarkan alasan simetri
Karena itu, berdasarkan alasan simetri
dan persamaan kita mengasumsikan bentuk
 Karena itu, berdasarkan alasan simetri
Karena itu, berdasarkan alasan simetri dan persamaan kita mengasumsikan bentuk
Adapun penafsiran persamaan - persamaan itu kita buat pengandaian : Misalkan sebuah titik muatan listrik mempunyai besar (magnitude) "satu" jika diukur dalam sistem stasioner, yakni jika diam dalam sistem stasioner ia mengerjakan gaya sebesar satu dyne pada muatan lain yang sama besar pada jarak satu sentimeter. Berdasarkan prinsip relativitas, muatan listrik ini juga mempunyai besar "satu" jika diukur dalam sistem bergerak. Jika besaran listrik ini pada saat diam relatif terhadap sistem stasioner, maka dengan definisi vektor (X, Y, Z) adalah sama dengan gaya yang bekerja padanya. Dan jika besaran listrik ini diam relatif terhadap sistem bergerak (setidaknya pada saat yang tepat), maka gaya yang bekerja padanya jika diukur dari sistem yang bergerak adalah sama dengan vektor (X', Y', Z'). Kensekuensinya, ketiga persamaan pertama di atas mengizinkan "diri mereka" untuk dinyatakan dalam dua jalan berikut :
- Jika satu unit titik muatan listrik bergerak dalam medan elektromagnetik, akan didapati beberapa aksi, di antaranya adalah gaya listrik disamping "gaya gerak listrik" yang mana jika kita mengabaikan suku - suku yang mempunyai pangkat dua atau lebih untuk υ/c, sama dengan hasil kali vektor kecepatan muatan dengan gaya magnet dibagi kecepatan cahaya. (Pernyataan cara lama)
- Jika satu unit titik muatan listrik bergerak dalam medan elektromagnetik, gaya yang bekerja terhadapnya sama dengan gaya listrik yang hadir pada lokalitas muatan, dan yang kita pastikan menggunakan transformasi medan ke dalam sistem koordinat diam relatif terhadap muatan elektrik itu. (Pernyataan cara baru)
Analogi yang sesuai dengan "gaya gerak magnet". Kita tahu bahwa gaya gerak listrik hanya memainkan peran tambahan dalam konsepsi teori yang dikembangkan, yang mengharuskan sebuah definisi pada lingkungan sekitarnya, bahwa gaya - gaya listrik dan magnet tidak bebas terhadap keadaan gerak sistem koordinat tersebut.
Lebih lanjut lagi, telah jelas bahwa ketidak simetrian (asimetry) yang disebutkan dalam pendahuluan seperti yang timbul ketika kita mempertimbangkan arus yang diproduksi oleh gerak relatif magnet dan konduktor, sekarang tidak tampak. Terlebih, pertanyaan - pertanyaan seperti "tempat duduk (seat)" elektrodinamika bagi gaya gerak listrik (mesin banyak kutub) sekarang tidak punya landasan.
§ 7. Teori Prinsip Doppler dan Penyimpangan (Aberration)
Dalam sistem K, dalam jarak yang sangat jauh dari pusat koordinat, misalkan di sana terdapat sumber gelombang elektromagnetik yang mana dalam potongan ruang yang memuat titik asal itu dapat digambarkan dengan derajat pendekatan yang cukup oleh persamaan berikut
dimana
di sini ( ) dan (
) dan ( ) adalah vektor - vektor yang mendefinisikan amplitudo deret-gelombang, dan l, m, n, adalah kosinus arah dari normal-gelombang. Kita ingin tahu hukum gelombang - gelombang itu, jika mereka ditinjau oleh pengamat diam dalam sistem bergerak k.
) adalah vektor - vektor yang mendefinisikan amplitudo deret-gelombang, dan l, m, n, adalah kosinus arah dari normal-gelombang. Kita ingin tahu hukum gelombang - gelombang itu, jika mereka ditinjau oleh pengamat diam dalam sistem bergerak k.
 ) dan (
) dan ( ) adalah vektor - vektor yang mendefinisikan amplitudo deret-gelombang, dan l, m, n, adalah kosinus arah dari normal-gelombang. Kita ingin tahu hukum gelombang - gelombang itu, jika mereka ditinjau oleh pengamat diam dalam sistem bergerak k.
) adalah vektor - vektor yang mendefinisikan amplitudo deret-gelombang, dan l, m, n, adalah kosinus arah dari normal-gelombang. Kita ingin tahu hukum gelombang - gelombang itu, jika mereka ditinjau oleh pengamat diam dalam sistem bergerak k.Dengan menerapkan persamaan transformasi yang diperoleh dalam § 6 untuk gaya listrik dan magnet, juga persamaan dalam § 3 untuk koordinat ruang dan waktu, langsung kita dapatkan
dimana
Dari persamaan w', didapatkan bahwa jika seorang pengamat bergerak dengan kecepatan υ relatif terhadap jarak tak hingga tempat sumber cahaya dengan frekuensi ν, sedemikian sehingga garis yang menghubungkan "sumber-pengamat" membentuk sudut Φ dengan kecepatan pengamat yang teracu pada sistem koordinat yang diam relatif terhadap sumber, frekuensi cahaya ν' yang dilihat pengamat diberikan oleh persamaan
Inilah Prinsip Doppler untuk semua kecepatan. Jika Φ = 0 persamaan dapat berbentuk
Kita tahu bahwa, berbeda dengan pandangan biasa, jika υ = -c, ν' = ~.
Jika sudut antara normal gelombang (arah sinar) dalam sistem bergerak dan garis penghubung "sumber-pengamat" adalah Φ', persamaan untuk Φ[*6] mengasumsikan bentuk
Persamaan ini menyatakan hukum aberasi dalam bentuk yang paling umum. Jika Φ = π/2, persamaan menjadi sederhana
Kita masih harus menemukan amplitudo gelombang, sebagaimana ia tampak dalam sistem bergerak. Jika amplitudo gaya listrik dan magnet masing - masing kita sebut A dan A', sebagaimana diukur dalam sistem stasioner maupun sistem bergerak, kita dapatkan
yang mana persamaan itu, jika Φ = 0, dapat disederhanakan menjadi
Dari hasil ini didapat pernyataan bahwa pengamat yang mendekati sumber dengan kecepatan sebesar c, maka akan tampak olehnya sumber cahaya mempunyai intensitas yang tak terbatas.
§ 8. Transformasi Energi Sinar Cahaya. Teori Tekanan Radiasi yang Diberikan pada Pemantul Sempurna
Karena  sama dengan energi cahaya per satuan volume, kita harus menganggap
sama dengan energi cahaya per satuan volume, kita harus menganggap  (dengan prinsip relativitas) sebagai energi cahaya dalam sistem bergerak. Dengan demikian
(dengan prinsip relativitas) sebagai energi cahaya dalam sistem bergerak. Dengan demikian  akan menjadi perbandingan antara energi cahaya pada "pegukuran dalam sistem bergerak" dan "pengukuran dalam sistem diam", jika volume cahaya sama baik jika diukur di K maupun k. Tapi bukan ini masalahnya. Jika l, m, n adalah kosinus arah dari normal gelombang cahaya dalam sistem stasioner, maka tidak ada energi yang melewati permukaan elemen permukaan sferis yang bergerak dengan kecepatan cahaya :-
akan menjadi perbandingan antara energi cahaya pada "pegukuran dalam sistem bergerak" dan "pengukuran dalam sistem diam", jika volume cahaya sama baik jika diukur di K maupun k. Tapi bukan ini masalahnya. Jika l, m, n adalah kosinus arah dari normal gelombang cahaya dalam sistem stasioner, maka tidak ada energi yang melewati permukaan elemen permukaan sferis yang bergerak dengan kecepatan cahaya :-
 sama dengan energi cahaya per satuan volume, kita harus menganggap
sama dengan energi cahaya per satuan volume, kita harus menganggap  (dengan prinsip relativitas) sebagai energi cahaya dalam sistem bergerak. Dengan demikian
(dengan prinsip relativitas) sebagai energi cahaya dalam sistem bergerak. Dengan demikian  akan menjadi perbandingan antara energi cahaya pada "pegukuran dalam sistem bergerak" dan "pengukuran dalam sistem diam", jika volume cahaya sama baik jika diukur di K maupun k. Tapi bukan ini masalahnya. Jika l, m, n adalah kosinus arah dari normal gelombang cahaya dalam sistem stasioner, maka tidak ada energi yang melewati permukaan elemen permukaan sferis yang bergerak dengan kecepatan cahaya :-
akan menjadi perbandingan antara energi cahaya pada "pegukuran dalam sistem bergerak" dan "pengukuran dalam sistem diam", jika volume cahaya sama baik jika diukur di K maupun k. Tapi bukan ini masalahnya. Jika l, m, n adalah kosinus arah dari normal gelombang cahaya dalam sistem stasioner, maka tidak ada energi yang melewati permukaan elemen permukaan sferis yang bergerak dengan kecepatan cahaya :-Karena itu dapat kita katakan bahwa permukaan ini membungkus cahaya yang sama secara permanen. Mari kita selidiki besaran energi yang terbungkus oleh permukaan ini jika dilihat dari sistem k, yaitu energi cahaya relatif terhadap sistem k.
Permukaan sferis -jika dilihat dari sistem bergerak- merupakan permukaan elipsoida, persamaan yang menyatakan hal itu pada saat τ = 0 adalah
Jika S adalah volume bola, dan S' volume elipsoid itu, maka dengan perhitungan sederhana
Dengan demikian, jika energi cahaya yang terlingkupi permukaan ini kita sebut E jika diukur dalam sistem stasioner, dan E' jika diukur dalam sistem bergerak, kita dapatkan
dan rumusan ini, jika Φ = 0, dapat diederhanakan menjadi
Sungguh luar biasa, energi dan frekuensi cahaya mempunyai perbedaan ketika diukur oleh pengamat yang diam dan bergerak sedangkan keduanya tunduk pada hukum yang sama.
Sekarang misalkan koordinat bidang ξ = 0 menjadi permukaan yang memantulkan cahaya secara sempurna, di mana gelombang datar yang digagas dalam § 7 dipantulkan. Kita cari tekanan yang diberikan cahaya pada permukaan pemantul, arah, frekuensi dan intensitas cahaya pasca pemantulan.
Misalkan cahaya yang identik (dengan cahaya sebelumnya) didefinisikan oleh besaran - besaran A, cos Φ dan ν yang teracu pada sistem K. Ditinjau dari k, besaran - besaran yang bersesuaian adalah
Untuk cahaya yang dipantulkan, teracu pada sistem k, kita dapatkan
Terakhir, dengan mentransformasikan kembali ke sistem stasioner K, kita peroleh persamaan - persamaan berikut untuk cahaya yang dipantulkan
Energi (yang diukur dalam sistem stasioner) yang membentur satu satuan luas per satuan waktu pada cermin :  . Sedangkan energi yang meninggalkan satu satuan luas per satuan waktu :
. Sedangkan energi yang meninggalkan satu satuan luas per satuan waktu :  . Perbedaan dari kedua pernyataan ini adalah, berdasarkan prinsip energi, usaha yang dilakukan oleh tekanan cahaya per satuan waktu. Jika kita menyusun "usaha" ini sebagai hasil kali Pv, dimana P adalah tekanan cahaya, kita dapatkan
. Perbedaan dari kedua pernyataan ini adalah, berdasarkan prinsip energi, usaha yang dilakukan oleh tekanan cahaya per satuan waktu. Jika kita menyusun "usaha" ini sebagai hasil kali Pv, dimana P adalah tekanan cahaya, kita dapatkan
 . Sedangkan energi yang meninggalkan satu satuan luas per satuan waktu :
. Sedangkan energi yang meninggalkan satu satuan luas per satuan waktu :  . Perbedaan dari kedua pernyataan ini adalah, berdasarkan prinsip energi, usaha yang dilakukan oleh tekanan cahaya per satuan waktu. Jika kita menyusun "usaha" ini sebagai hasil kali Pv, dimana P adalah tekanan cahaya, kita dapatkan
. Perbedaan dari kedua pernyataan ini adalah, berdasarkan prinsip energi, usaha yang dilakukan oleh tekanan cahaya per satuan waktu. Jika kita menyusun "usaha" ini sebagai hasil kali Pv, dimana P adalah tekanan cahaya, kita dapatkanDalam penyesuaiannya dengan eksperimen dan teori - teori lain, pendekatan pertama kita dapatkan
Semua masalah dalam optika benda bergerak dapat diselesaikan dengan metode yang digunakan di sini. Yang penting, gaya listrik dan magnet dari cahaya yang dipengaruhi oleh benda bergerak, dapat ditransformasikan menjadi sistem koordinat diam relatif terhadap benda itu. Dengan begini, semua permasalahan dalam optika benda bergerak bisa dipersempit ke dalam serentetan kasus optika benda diam.
§ 9. Transformasi Persamaan Maxwell-Hertz Ketika Arus Konveksi Diperhitungkan
Kita mulai dari persamaan ini
dimana
menyatakan 4π kali rapat listrik, dan ( ) merupakan vektor kecepatan muatan. Jika kita bayangkan muatan listrik termuat dalam benda tegar yang kecil (ion atau elektron misalnya), maka persamaan - persamaan tersebut merupakan elektromagnetika dasar untuk elektrodinamika dan optika Lorentzian dari benda bergerak.
) merupakan vektor kecepatan muatan. Jika kita bayangkan muatan listrik termuat dalam benda tegar yang kecil (ion atau elektron misalnya), maka persamaan - persamaan tersebut merupakan elektromagnetika dasar untuk elektrodinamika dan optika Lorentzian dari benda bergerak.
 ) merupakan vektor kecepatan muatan. Jika kita bayangkan muatan listrik termuat dalam benda tegar yang kecil (ion atau elektron misalnya), maka persamaan - persamaan tersebut merupakan elektromagnetika dasar untuk elektrodinamika dan optika Lorentzian dari benda bergerak.
) merupakan vektor kecepatan muatan. Jika kita bayangkan muatan listrik termuat dalam benda tegar yang kecil (ion atau elektron misalnya), maka persamaan - persamaan tersebut merupakan elektromagnetika dasar untuk elektrodinamika dan optika Lorentzian dari benda bergerak.Misalkan persamaan - persamaan itu sah untuk sistem K, dan transformasikan mereka, dengan bantuan persamaan yang diberikan dalam § 3 dan § 6, pada sistem k. Kita peroleh persamaan - persamaan berikut
dimana
dan
Karena -mengikuti teorema penjumlahan kecepatan (§ 5)- vektor  tidak lain kecuali kecepatan muatan listrik, yang diukur dalam sistem k, kita telah membuktikan hal itu, berdasarkan prinsip kinematika, pondasi elektrodinamika teori Lorentz untuk elektrodinamikan benda - benda bergerak adalah sesuai dengan prinsip relativitas. Sebagai tambahan Saya akan memberi komentar singkat, bahwa hukum penting berikut dengan mudah dapat diturunkan dari persamaan - persamaan yang telah dikembangkan: Jika sebuah benda bermuatan listrik bergerak di sebarang tempat dalam ruang tanpa terdekteksi adanya perubahan muatan jika ditinjau dari sistem koordinat yang bergerak dengan benda itu, maka jika ditinjau dari sistem stasioner pun muatannya tidak berubah.
tidak lain kecuali kecepatan muatan listrik, yang diukur dalam sistem k, kita telah membuktikan hal itu, berdasarkan prinsip kinematika, pondasi elektrodinamika teori Lorentz untuk elektrodinamikan benda - benda bergerak adalah sesuai dengan prinsip relativitas. Sebagai tambahan Saya akan memberi komentar singkat, bahwa hukum penting berikut dengan mudah dapat diturunkan dari persamaan - persamaan yang telah dikembangkan: Jika sebuah benda bermuatan listrik bergerak di sebarang tempat dalam ruang tanpa terdekteksi adanya perubahan muatan jika ditinjau dari sistem koordinat yang bergerak dengan benda itu, maka jika ditinjau dari sistem stasioner pun muatannya tidak berubah.
 tidak lain kecuali kecepatan muatan listrik, yang diukur dalam sistem k, kita telah membuktikan hal itu, berdasarkan prinsip kinematika, pondasi elektrodinamika teori Lorentz untuk elektrodinamikan benda - benda bergerak adalah sesuai dengan prinsip relativitas. Sebagai tambahan Saya akan memberi komentar singkat, bahwa hukum penting berikut dengan mudah dapat diturunkan dari persamaan - persamaan yang telah dikembangkan: Jika sebuah benda bermuatan listrik bergerak di sebarang tempat dalam ruang tanpa terdekteksi adanya perubahan muatan jika ditinjau dari sistem koordinat yang bergerak dengan benda itu, maka jika ditinjau dari sistem stasioner pun muatannya tidak berubah.
tidak lain kecuali kecepatan muatan listrik, yang diukur dalam sistem k, kita telah membuktikan hal itu, berdasarkan prinsip kinematika, pondasi elektrodinamika teori Lorentz untuk elektrodinamikan benda - benda bergerak adalah sesuai dengan prinsip relativitas. Sebagai tambahan Saya akan memberi komentar singkat, bahwa hukum penting berikut dengan mudah dapat diturunkan dari persamaan - persamaan yang telah dikembangkan: Jika sebuah benda bermuatan listrik bergerak di sebarang tempat dalam ruang tanpa terdekteksi adanya perubahan muatan jika ditinjau dari sistem koordinat yang bergerak dengan benda itu, maka jika ditinjau dari sistem stasioner pun muatannya tidak berubah.§ 10. Dinamika Elektron yang Dipercepat Perlahan - Lahan
Misalkan terdapat sebuah partikel bermuatan listrik (yang sebelumnya kita sebut elektron) bergerak dalam medan elektromagnetik, yang mana hukumnya kita asumsikan sebagai berikut :
Jika elektron tersebut diam pada waktu tertentu, gerak elektron pada waktu selanjutnya diberikan oleh persamaan
dimana x, y, z menyatakan koordinat elektron dan m untuk massa-nya selagi geraknya cukup lambat.
Sekarang, misalkan kecepatan elektron pada saat tertentu adalah υ. Kita cari hukum gerak elektron sesaat sesudahnya. Tanpa mempengaruhi topik umum pembahasan kita, kita bisa dan akan mengasumsikan bahwa elektron, ketika kita perhatikan, berada di titik pusat koordinat dan bergerak dengan kecepatan υ sepanjang sumbu X dari sistem K. Maka jelas bahwa pada saat yang diberikan (t = 0) elektron diam relatif terhadap sistem koordinat yang bergerak seragam dengan kecepatan υ sepanjang sumbu X.
Dari asumsi di atas, dalam kombinasinya dengan prinsip relativitas , telah jelas bahwa untuk waktu sesaat (nilai yang kecil untuk t) elektron yang ditinjau dari sistem k bergerak sesuai persamaan
dimana simbol - simbol ξ, η, ζ, X’, Y’, Z’ teracu pada sistem k. Lebih lanjut, jika kita putuskan bahwa ketika t = x = y = z = 0 maka τ = ξ = η = ζ = 0 persamaan transformasi § 3 dan § 6 berlaku, sehingga kita punya
Dengan bantuan persamaan - persamaan itu kita transformasikan persamaan gerak di atas dari sistem k ke K, dan didapat
Dengan mengambil sudut pandang biasa sekarang kita kita cari "longitudinal" dan transversal massa elektron yang bergerak. Kita tulis persamaan (A) dalam bentuk
dan terlebih dahulu kita sepakati bahwa  adalah komponen - komponen gaya gerak yang bekerja pada elektron, seperti yang terlihat dalam sistem bergerak pada saat yang sama dengan elektron, dan dengan kecepatan yang sama pula. (Gaya ini dapat diukur, misalnya, dengan menggunakan neraca pegas yang diam dalam sistem yang disebutkan terakhir.) Sekarang jika kita sebut gaya ini secara sederhana "gaya yang bekerja pada elektron,"[9] dan mempertahankan persamaan -massa × percepatan = gaya- dan jika kita juga memutuskan bahwa percepatan itu dapat diukur dalam sistem stasioner K, maka kita turunkan persamaan - persamaan berikut dari persamaan di atas
adalah komponen - komponen gaya gerak yang bekerja pada elektron, seperti yang terlihat dalam sistem bergerak pada saat yang sama dengan elektron, dan dengan kecepatan yang sama pula. (Gaya ini dapat diukur, misalnya, dengan menggunakan neraca pegas yang diam dalam sistem yang disebutkan terakhir.) Sekarang jika kita sebut gaya ini secara sederhana "gaya yang bekerja pada elektron,"[9] dan mempertahankan persamaan -massa × percepatan = gaya- dan jika kita juga memutuskan bahwa percepatan itu dapat diukur dalam sistem stasioner K, maka kita turunkan persamaan - persamaan berikut dari persamaan di atas
 adalah komponen - komponen gaya gerak yang bekerja pada elektron, seperti yang terlihat dalam sistem bergerak pada saat yang sama dengan elektron, dan dengan kecepatan yang sama pula. (Gaya ini dapat diukur, misalnya, dengan menggunakan neraca pegas yang diam dalam sistem yang disebutkan terakhir.) Sekarang jika kita sebut gaya ini secara sederhana "gaya yang bekerja pada elektron,"[9] dan mempertahankan persamaan -massa × percepatan = gaya- dan jika kita juga memutuskan bahwa percepatan itu dapat diukur dalam sistem stasioner K, maka kita turunkan persamaan - persamaan berikut dari persamaan di atas
adalah komponen - komponen gaya gerak yang bekerja pada elektron, seperti yang terlihat dalam sistem bergerak pada saat yang sama dengan elektron, dan dengan kecepatan yang sama pula. (Gaya ini dapat diukur, misalnya, dengan menggunakan neraca pegas yang diam dalam sistem yang disebutkan terakhir.) Sekarang jika kita sebut gaya ini secara sederhana "gaya yang bekerja pada elektron,"[9] dan mempertahankan persamaan -massa × percepatan = gaya- dan jika kita juga memutuskan bahwa percepatan itu dapat diukur dalam sistem stasioner K, maka kita turunkan persamaan - persamaan berikut dari persamaan di atasDengan perbedaan definisi gaya dan percepatan, secara alami kita akan mendapatkan nilai - nilai yang berlainan untuk massa. Hal ini menunjukkan bahwa dalam membandingkan teori - teori gerak eletron yang berbeda, kita harus melakukannya dengan sangat hati - hati.
Kita simpulkan bahwa hasil - hasil pengukuran massa itu juga sah untuk untuk sebarang titik materi bermassa, karena titik materi bermassa bisa dijadikan elektron (secara nalar) dengan menambahkan muatan listrik padanya, tak peduli seberapa pun kecilnya.
Sekarang kita tentukan energi kinetik elektron itu. Jika elektron bergerak dari keadaan diam pada titik asal koordinant sistem K sepanjang sumbu X di bawah aksi gaya listrik statis X, telah jelas bahwa energi yang didapat dari medan listrik statis itu bernilai  . Jika elektron dipercepat perlahan - lahan, sehingga tidak akan melepaskan energi dalam bentuk radiasi, maka energi yang didapat dari medan elektrostatik harus setara dengan energi gerak elektron W. Mengingat bahwa selama proses gerak yang kita tinjau, dengan menerapkan persamaan (A), karena itu kita dapatkan
. Jika elektron dipercepat perlahan - lahan, sehingga tidak akan melepaskan energi dalam bentuk radiasi, maka energi yang didapat dari medan elektrostatik harus setara dengan energi gerak elektron W. Mengingat bahwa selama proses gerak yang kita tinjau, dengan menerapkan persamaan (A), karena itu kita dapatkan
 . Jika elektron dipercepat perlahan - lahan, sehingga tidak akan melepaskan energi dalam bentuk radiasi, maka energi yang didapat dari medan elektrostatik harus setara dengan energi gerak elektron W. Mengingat bahwa selama proses gerak yang kita tinjau, dengan menerapkan persamaan (A), karena itu kita dapatkan
. Jika elektron dipercepat perlahan - lahan, sehingga tidak akan melepaskan energi dalam bentuk radiasi, maka energi yang didapat dari medan elektrostatik harus setara dengan energi gerak elektron W. Mengingat bahwa selama proses gerak yang kita tinjau, dengan menerapkan persamaan (A), karena itu kita dapatkanDengan demikian, ketika υ = c, W menjadi tak terbatas. Kecepatan - kecepatan yang lebih besar besar dari kecepatan cahaya -sesuai hasil yag kita dapatkan sebelumnya- tidak mempunyai kemungkinan untuk eksis.
Pernyataan energi kinetik juga, berdasarkan argumen yang kita nyatakan di atas, harus bisa diterapkan dengan baik pada benda bermassa.
Sekarang kita akan menyebutkan sifat -sifat gerak elektron yang dihasilkan dari sistem persamaan (A), dan bisa dibuktikan melalui percobaan.
1. Dari persamaan kedua dari sistem (A) didapat bahwa gaya listrik Y dan gaya magnet N mempunyai aksi pembelokan yang sama kuatnya terhadap elektron yang bergera dengan kecepatan υ, jika  Dengan demikian kita tahu bahwa dengan teori kita dimungkinkan untuk menentukan kecepatan elektron dari perbandingan antara daya pembelokan magnet
Dengan demikian kita tahu bahwa dengan teori kita dimungkinkan untuk menentukan kecepatan elektron dari perbandingan antara daya pembelokan magnet  dengan daya mempelokan listrik
dengan daya mempelokan listrik  , untuk sebarang kecepatan, dengan menerapkan hukum
, untuk sebarang kecepatan, dengan menerapkan hukum
 Dengan demikian kita tahu bahwa dengan teori kita dimungkinkan untuk menentukan kecepatan elektron dari perbandingan antara daya pembelokan magnet
Dengan demikian kita tahu bahwa dengan teori kita dimungkinkan untuk menentukan kecepatan elektron dari perbandingan antara daya pembelokan magnet  dengan daya mempelokan listrik
dengan daya mempelokan listrik  , untuk sebarang kecepatan, dengan menerapkan hukum
, untuk sebarang kecepatan, dengan menerapkan hukumHubungan ini dapat diuji secara eksperimental, selagi kecepatan elektron dapat diukur secara langsung, misalnya dengan cara menggetarkan medan listrik dan magnet dengan cepat.
2. Dari deduksi untuk energi kinetik elektron didapat bahwa antara beda potensial, P, kecepatan transversal dan yang dicapai υ oleh elektron harus memenuhi hubungan
3. Kita hitung jari - jari kelengkungan lintasan elektron ketika terdapat gaya magnet N (sebagai satu-satunya gaya pembelok), bekerja secara tegak lurus terhadap kecepatan elektron. Dari persamaan kedua (A) kita dapatkan
atau
Hubungan - hubungan itu merupakan pernyataan lengkap tentang hukum - hukum yang, berdasarkan teori lanjutan di sini, menentukan gerak elektron.
Sebagai kesimpulan saya ingin mengatakan bahwa dalam menyelesaikan masalah - masalah dikemukakan di sini saya mendapat bantuan tulus dari teman dan sekaligus kolega saya M. Besso, dan bahwa saya berhutang budi padanya atas beberapa saran yang begitu berharga.
Catatan Kaki :
[1] Memoar sebelumnya oleh Lorentz pasa saat ini belum diketahui oleh penulis.
[2] Yakni pendekatan pertama.
[3] Di sini kita tidak akan mendiskusikan ketidaktepatan yang termuat dalam konsep simultanitas dua kejadian pada dua tempat yang berdekatan, yang hanya bisa dihapus dengan abstraksi.
[4] "Waktu" di sini menyatakan "waktu dalam sistem stasioner" dan juga "posisi jarum jam bergerak yang didiskusikan."
[5] Persamaan Transformasi Lorentz mungkin dideduksikan dengan lebih sederhana secara langsung dari kondisi bahwa dalam persamaan itu relasi  akan mempunyai konsekuensi hubungan kedua
akan mempunyai konsekuensi hubungan kedua  .
.
 akan mempunyai konsekuensi hubungan kedua
akan mempunyai konsekuensi hubungan kedua  .
.[6] Sebuah benda bebentuk bola jika ditinjau pada saat diam.
[7] Bukan jam bandul, dimana secara fisis merupakan sistem yang bergantung pada Bumi. Kasus ini harus ditiadakan.
[8] Jika, misalnya  , dan
, dan  , maka dari alasan simetri jelas bahwa jika υ berganti tanda tanpa merubah nilai numerik, Y' juga harus berganti tanda tanpa merubah nilai numeriknya.
, maka dari alasan simetri jelas bahwa jika υ berganti tanda tanpa merubah nilai numerik, Y' juga harus berganti tanda tanpa merubah nilai numeriknya.
 , dan
, dan  , maka dari alasan simetri jelas bahwa jika υ berganti tanda tanpa merubah nilai numerik, Y' juga harus berganti tanda tanpa merubah nilai numeriknya.
, maka dari alasan simetri jelas bahwa jika υ berganti tanda tanpa merubah nilai numerik, Y' juga harus berganti tanda tanpa merubah nilai numeriknya.[9] Definisi gaya yang diberikan di sini tidak berguna, sebagaimana pertama kali ditunjukkan oleh M. Planck. Lebih baik mendefinisikan gaya sedemikian rupa sehingga hukum - hukum momentum dan energi menempati bentuk yang lebih sederhana.
Catatan Editor
[*1] Dalam makalah asli Einstein, simbol - simbol (Ξ, H, Z) untuk koordinat sistem bergerak k diperkenalkan tanpa ada penjelasan eksplisit. Dalam terjemahan berbahasa Inggris tahun 1923 digunakan (X, Y, Z), yang menyebabkan timbulnya ambiguitas antara koordinat X dalam sistem K dan sumbu sejajar dalam sistem bergerak k. Di sini dan dalam acuan selanjutnya kami menggunakan Ξ ketika mengacu pada sistem k selagi sistem itu berhubungan dengan K. Sebagai tambahan, kerangka acuan sistem K', berikutnya dalam kalimat ini secara keliru diberikan oleh "k" dalam terjemahan Bahasa Inggris tahun 1923.
[*2] Dalam terjemahan asli dalam bahasa Inggris tahun 1923, fase ini kata ini diartikan secara keliru sebagai "bidang datar". Saya telah menggunakan terjemahan yang benar bagi "bidang datar" dalam dokumen ini.
[*3] Persamaan ini salah tulis baik dalam naskah asli Einstein maupun terjemahan berbahasa Inggris tahun 1923 sebagai ( ).
).
 ).
).[*4] Pangkat c milik suku sinus pada penyebut dalam persamaan ini salah tulis, dinyatakan sebagai 2 dalam terjemahan edisi Bahasa Inggris tahun 1923. Di sini telah dibetulkan.
[*5] "X" dalam edisi Bahasa Inggris 1923.
[*6] Secara keliru ditulis l' dalam terjemahan Bahasa Inggris tahun 1923, tetap diedarkan meskipun berubah tanda, dari makalah asli tahun 1905.
Artikel versi Bahasa Inggris-nya saya peroleh dari sini. Dan untuk perbandingan, pembaca bisa mendownload versi bahasa Jerman-nya di sini. Mohon maaf jika ada kesalahan dari segi apapun...
Artikel versi Bahasa Inggris-nya saya peroleh dari sini. Dan untuk perbandingan, pembaca bisa mendownload versi bahasa Jerman-nya di sini. Mohon maaf jika ada kesalahan dari segi apapun...