Gelombang berjalan dan gelombang stationer
Di postingan terdahulu telah dijelaskan bahwa salah satu atribut yang dimiliki gelombang adalah amplitudo. Nah, berdasarkan amplitudonya gelombang dapat dibagi menjadi dua, yaitu gelombang berjalan dan gelombang stasioner. Gelombang berjalan adalah gelombang yang amplitudonya selalu tetap. Contohnya gelombang sinusoidal (1). Sedangkan gelombang stasioner adalah gelombang yang amplitudonya tidak tetap. Hal ini disebabkan oleh beberapa faktor. Salah satunya, jika sebuah gelombang membentur “dinding” lantas dipantulkan kembali maka gelombang akan bertabrakan dan amplitudonya akan terpengaruh. Gelombang stasioner dibagi menjadi 2, yaitu ujung terikat dan ujung tetap.
Gelombang pada umumnya mempunyai sifat – sifat sebagai berikut :
Dapat dipantulkan (Refleksi)
Dapat dibiaskan (Refraksi), sifat ini tunduk pada hukum Snellius
Dapat dipadukan (Interferensi)
Dapat dilenturkan melalui celah sempit (Difraksi)
Dapat diserap arah getarnya (Polarisasi)
Persamaan gerak
Karena gerak gelombang merupakan gerak harmonik, maka penurunan persamaan geraknya dapat dilakukan dengan menganalisa gerak melingkar. Perhatikan gambar berikut :
Sebuah titik pada saat
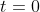
(bukan pusat koordinat) berada di
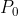
, kemudian bergerak ke titik
. Lintasan gerak ini diproyeksikan ke garis
, sehingga menghasilkan simpangan
atau proyeksinya
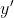
. Nilai
paling tinggi adalah jari – jari lingkaran,
. Kita peroleh :
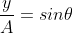
atau
.
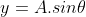
Untuk berputar penuh, dibutuhkan waktu sebesar
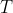
. Tapi
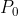
hanya bergerak sampai
, maka waktu tempuh yang diperlukan titik ini adalah :
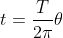
, atau
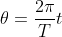
. Maka
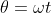
. jadi
.
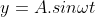
Kecepatan Getar
Laju partikel yang bergerak melingkar adalah tetap, sedangkan arahnya selalu berubah. Dilukiskan oleh vektor
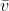
. Besar
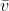
= keliling lingkaran / periode =
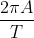
. Ingat, A = amplitudo = jari – jari lingkaran. Kecepatan getar dilukiskan oleh proyeksi
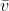
pada garis BC, yaitu
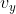
. Diberikan oleh rumus :
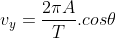
atau
.
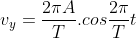
Kecepatan titik proyeksi P, jika :
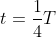
maka P’ berada di B, cos 90 = 0 ,
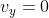
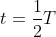
maka P’ berada di O, cos 180 = -1 ,
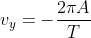
(tanda “-” menunjukkan arah ke bawah)
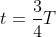
, maka P’ berada di C, cos 270 = 0 ,
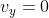
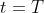
, maka P’ berada di O, cos 360 = cos 0 = 1 ,
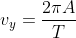
(arah ke atas)
Kesimpulan :
Jika simpangan mencapai nilai ekstrimnya maka kecepatan getar sama dengan nol.
Jika simpangan berada pada titik kesetimbangan, maka kecepatannya mencapai harga ekstrim.
Percepatan
Titik P yang kita tinjau, seharusnya bergerak dengan kecepatan sebesar
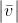
lurus. Kenyataannya ia bergerak mengintari pusat lingkaran, seolah – olah ada yang menarik ke pusat. Tarikan ini selanjutnya didefinisikan sebagai percepatan yang besarnya tetap sedangkan arahnya selau menuju pusat lingkaran. Percepatan ini disebut percepatan sentripetal. Besarnya diberikan oleh rumus :
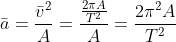
. Percepatan getarnya diberikan oleh proyeksi
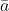
pada garis BC yaitu
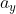
. Besarnya :
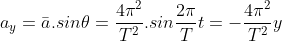
Faktor -1 muncul dari perkalian vektor yang menunjukan bahwa arah percepatan sentripetal selalu berlawanan dengan arah simpangan.
Jika :
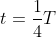
maka P’ berada di B,
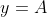
dan
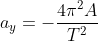
(arah ke bawah)
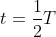
maka P’ berada di O,
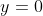
dan
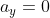
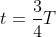
, maka P’ berada di C,
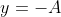
dan
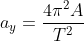
(arah ke atas)
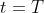
, maka P’ berada di O,
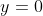
dan
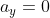
Kesimpulan:
Setiap benda yang melakukan getaran selaras akan mengalami gaya yang besarnya sebanding dengan simpangan, namun arahnya selalu menuju ke arah titik setimbang.
Kalkulus Beraksi
Persamaan di atas dapat juga diperoleh melalui teknik kalkulus diferensial. Seperti biasanya, turunan pertama dari fungsi posisi adalah fungsi kecepatan sedangkan turunan keduanya merupakan fungsi percepatan.
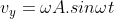
=> fungsi posisi
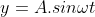
=> fungsi kecepatan (turunan pertama)
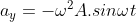
=> fungsi percepatan (turunan kedua)
Nampak diperoleh hasil yang sama dengan metode analisa gerak
Persamaan Gelombang Berjalan
Garis merah G1 menggambarkan gelombang yang merambat dari kiri ke kanan pada saat tertentu, misalkan cepat rambat gelombang ini adalah v. sedangkan garis hijau G2 merupakan keadaan gelombang tadi setelah t detik. Perhatikan juga, di sana terdapat titik pembatas untuk memudahkan analisa. Titik O di pusat koordinat dan titik P di ujung gelombang berimpit dengan sumbu-x. Saat O mulai bergetar, P masih diam. Hingga beberapa saat kemudian, ketika O telah bergetar selama t detik barulah P mulai bergetar. Kesimpulannya, ketika O telah berosilasi selama t detik maka P juga berosilasi selama kurang dari t detik.
Simpangan di titik O diberikan oleh persamaan :
Sementara titik P yang waktu getarnya kurang dari O, yakni sebesar x/v detik akan memiliki simpangan :
Jika gelombang bergereak dari kanan ke kiri, ketika O sudah bergetar selama t detik maka P telah bergetar selama
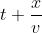
detik. Dengan carayang sama diperoleh :
Karena kedua persamaan hanya berbeda tanda, maka kita dapat membuat rumusan yang lebih umum :
.
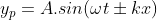Persamaan gerak gelombang klasik
Perhatikan bahwa nilai y tergantung pada posisinya dalam sumbu-x, dan tentu saja waktu. Maka fungsi gelombang secara umum adalah y = f(x,t). Sekaligus juga memenuhi persamaan
dimana suku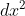 
setara dengan 
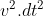. Dan, tanda 
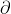diganti dengan d karena persamaan tersebut merupakan fungsi dengan variabel tunggal. Perasamaan inilah yang selanjutnya digunakan oleh Schrodinger untuk mendasari teorinya tentang fisika kuantum.
(1) Grafik fungsi sinus membentuk gelombang berjalan, karena itulah dinamakan gelombang sinusoidal.
