Terdapat masalah - masalah fisika yang membutuhkan nilai stasioner (puncak) dari suatu persamaan integral fungsional (fungsi di dalam fungsi). Tinjau persamaan berikut :
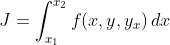
... (1)
dengan :
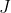
: Kuantitas yang ditentukan bernilai stasioner.
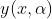
: sebuah fungsi (tepatnya kelas fungsi) dari

dan

.
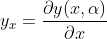
: turunan

terhadap

.

: variabel bebas.
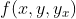
diketahui, namun ketergantungannya terhadap

dan

, yakni
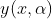
tidak diketahui. Artinya lintasan eksak
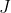
tidak diketahui kendati batas - batas integralnya
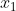
dan
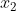
. Misi kita adalah mencari

sedemikian sehingga nilai
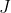
stasioner. Ini lebih rumit dari kalkulus biasa karena ada kemungkinan persamaan (1) tidak punya solusi.
Tentunya terdapat tak berhingga lintasan yang mungkin, yang memenuhi persamaan (1). Dua di antaranya dapat dilihat pada gambar 1.
Gambar 1 : Variasi Lintasan
Secara umum, persamaan yang menggambarkan lintasan - lintasan ini adalah
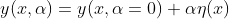
...(2)
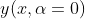
adalah kurva terpendek (ekstremal),

faktor skala, dan
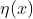
sebarang fungsi

yang menggambarkan perubahan bentuk lintasan serta memiliki titik awal dan akhir yang sama. Jadi
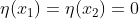
. Selain itu
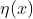
harus terdiferensial, otomatis
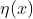
kontinu.
Sekarang kita definisikan beda lintasan - lintasan itu, dilambangkan dengan
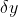
.
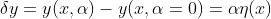
...(3)
kembali ke persamaan (1)
![J(\alpha) = \int_{x_1}^{x_2}\left [ y(x,\alpha), y(x, \alpha = 0) ,x \right ]dx](http://latex.codecogs.com/gif.latex?J%28%5Calpha%29%20=%20%5Cint_%7Bx_1%7D%5E%7Bx_2%7D%5Cleft%20[%20y%28x,%5Calpha%29,%20y%28x,%20%5Calpha%20=%200%29%20,x%20%5Cright%20]dx)
...(4)
Kondisi ekstrim diperoleh dari
yang analog dengan
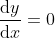
dalam kalkulus differensial. Penurunan secara parsial mengubah bentuk integran

menjadi
dari persamaan (2) kita peroleh
sehingga
![\frac{\partial J}{\partial \alpha} = \int_{x_1}^{x_2} \left [ \frac{\partial f}{\partial y}.\eta (x) + \frac{\partial f}{\partial y_x}.\frac{\mathrm{d} \eta(x)}{\mathrm{d} x} \right ]dx](http://latex.codecogs.com/gif.latex?%5Cfrac%7B%5Cpartial%20J%7D%7B%5Cpartial%20%5Calpha%7D%20=%20%5Cint_%7Bx_1%7D%5E%7Bx_2%7D%20%5Cleft%20[%20%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20y%7D.%5Ceta%20%28x%29%20+%20%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20y_x%7D.%5Cfrac%7B%5Cmathrm%7Bd%7D%20%5Ceta%28x%29%7D%7B%5Cmathrm%7Bd%7D%20x%7D%20%5Cright%20]dx)
...(5)
Ambil suku kedua untuk diintegrasikan secara parsial
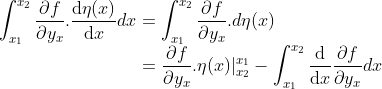
...(6)
suku pertama lenyap karena
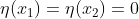
, jadi dengan mengembalikan hasil ini ke persamaan (5)
![\int_{x_1}^{x_2} \left [ \frac{\partial f}{\partial y}.\eta(x) - \frac{\mathrm{d} }{\mathrm{d} x}\frac{\partial f}{\partial y_x}.\eta(x) \right ]dx = \int_{x_1}^{x_2} \left [ \frac{\partial f}{\partial y} - \frac{\mathrm{d} }{\mathrm{d} x}\frac{\partial f}{\partial y_x} \right ]\eta(x) dx = 0](http://latex.codecogs.com/gif.latex?%5Cint_%7Bx_1%7D%5E%7Bx_2%7D%20%5Cleft%20[%20%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20y%7D.%5Ceta%28x%29%20-%20%5Cfrac%7B%5Cmathrm%7Bd%7D%20%7D%7B%5Cmathrm%7Bd%7D%20x%7D%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20y_x%7D.%5Ceta%28x%29%20%5Cright%20]dx%20=%20%5Cint_%7Bx_1%7D%5E%7Bx_2%7D%20%5Cleft%20[%20%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20y%7D%20-%20%5Cfrac%7B%5Cmathrm%7Bd%7D%20%7D%7B%5Cmathrm%7Bd%7D%20x%7D%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20y_x%7D%20%5Cright%20]%5Ceta%28x%29%20dx%20=%200)
...(7)
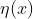
sebarang, karenanya kita mengambil integran persamaan (7) sama dengan nol, yakni

...(8)
yang dikenal dengan persamaan Euler-Lagrange (dalam bentuk yang paling sederhana). Untuk mencari
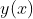
yang berasal dari persamaan integral stasioner cukup dengan mengolah integrannya dengan persamaan (8).
Bentuk berikut adalah alternatif lain dari persamaan Euler-Lagrange yang kadang berguna :
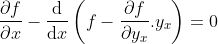
,
yakni didapat dari pengertian turunan total
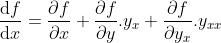
.
Sumber :
Arfken, George B. Weber, Hans J. 2005,
Mathematical Methods for Physicist 6th Edition, Elseiver Academic Press, California, USA.








30 Mei 2016 pukul 19.13
Thanks yah atas pencerahannya.