NARASOMA NOTEBOOK: Alihragam Legendre

Alihragam Legendre

0 komentar
Posted in Label: Catatan Kuliah, Kalkulus, Legendre, Matematika untuk Fisika

Diberikan suatu fungsi berpeubah tunggal $f(x)$ , yang mempunyai diferensial total

$df = p(x)dx$

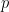
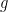
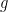
dengan $p(x) = f'(x)$ . Fungsi $p$ memberikan harga kemiringan $f$ di setiap titik ( $x,f(x)$ ). Hendak dicari suatu fungsi yang setara dengan $f$ , yakni fungi $g$ dengan informasi serupa $f$ , tetapi hanya bergantung pada peubah $p = f'(x)$ . Jadi, diharapkan ada fungsi $g$ yang dapat dihitung dari $f$ dan sebaliknya tanpa memunculkan sifat ambigu.

Gambar 1 ; Grafik fungsi $\tiny f$ berikut garis lurus yang menyinggung fungsi tersebut di titik $\tiny (x_0,f(x_0))$ .

Gambar di atas menunjukkan bahwa garis yang menyinggung fungsi $f$ di titik $(x_0,f(x_0))$ memenuhi persamaan berikut

$T_{x_0}(x) = f(x_0) +f'(x_0)(x-x_0)$

Didefinisikan $g(x) = T_x(0)$ . Karena itu diperoleh

$g(x) = f(x) - xf'(x) = f(x) - xp$

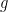
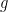
Dengan kata lain, fungsi $g$ adalah suatu fungsi yang memberikan harga kemiringan $f$ di setiap titik $(x,f(x))$ Orang menyebut fungsi $g$ sebagai alihragam Legendre bagi $f$ untuk semua nilai $x$ .

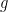
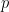
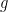
Sekarang, akan ditunjukkan bahwa nilai $g$ hanya bergantung pada $p$ . Untuk melakukan itu, $g$ didiferensialkan sehingga diperoleh

$dg = df -pdx -xdp = -xdp$

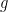
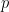
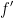
Adapun untuk mengetahui nilai $g$ di $p$ secara eksplisit, terlebih dahulu orang harus memastikan bahwa $f'$ mempunyai invers $f'^{-1}$ . Peubah $x$ tidak lain adalah $f'^{-1}(p)$ . Maka

$g(p) = f(f'^{-1}(p)) - f'^{-1}(p)p$

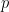
yang secara eksplisit hanya gayut pada $p$ . Maka orang dapat mengambil kesimpulan bahwa suatu fungsi $f$ dengan peubah $x$ mempunyai alihragam Legendre secara tunggal jika dan hanya jika $p = f'(x)$ mempunyai nilai tunggal untuk setiap $x$ . Berdasarkan pemahaman kita pada kalkulus, kita tahu bahwa fungsi $f$ harus melulu secara kaku (strictly monotonic) agar $p = f'(x)$ mempunyai invers. 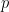Jika ada dua atau lebih $x$ yang berbagi harga $p$ , maka tentu alihragam Legendrenya tidak tunggal, bahkan boleh jadi tidak terdefinisi. Akan tetapi daerah asal fungsi $f$ dapat dibatasi pada nilai - nilai yang mengakibatkan $p = f'(x)$ mempunyai invers. Fungsi semacam ini dikatakan mempunyai alihragam Legendre perpotong.

-------------------------------------------------------------------------------
Contoh
1. Tentukan alihragam Legendre untuk fungsi sederhana $f(x) = x^2$ .
2.Tentukan alihragam Legendre untuk fungsi sederhana $f(x) = x$ .

Selesaian :
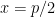
1. $p = f'(x) = 2x$ , atau $x=p/2$ . Maka alihragam Legendre untuk fungsi di atas adalah

$g (p) = x^2 - px$

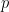
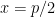
yang kegayutannya terhadap peubah $p$ secara eksplisit dapat diperoleh dengan menyisipkan harga $x=p/2$ , yakni

$g(p) = -p^2/4$

2. $p = f'(x) = 1$ , persamaan ini tidak dapat diselesaikan untuk $x$ . Secara "formal", alihragam Legendrenya adalah

$g(p) = x -px = x -x = 0$

yakni, tidak memuat informasi serupa dengan $f$ .

--------------------------------------------------------------------------------

Selanjutnya akan ditunjukkan bahwa, ketika diberikan alihragam Legendre bagi suatu fungsi, orang dapat menjalankan suatu algoritma tunggal untuk mendapatkan fungsi semula dari alihragam Legendre tersebut. Ingat kembali

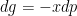
$g(p) = f(p) - xp$ dan $dg = -xdp$

yang memberikan

$f(p) = g(p) + xp$ serta $x = -g'(p)$

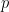
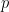
Peubah $p$ hendak digantikan oleh peubah $x$ secara tunggal. Ketika $f'(x)$ melulu, maka $x = -g'(p)$ juga melulu, sehingga persamaan ini dapat diselesaikan untuk $p$ . Jadi

$f(x) = g(-g'(p)) + x(-g'(p))$

sehingga diperoleh kembali fungsi awal $f$ .

Perampatan
Perampatan alihragam Legendre ke fungsi berpeubah banyak tidak membutuhkan langkah khusus. Misalkan $f(x,y)$ diberikan, maka

$df = p(x,y)dx + q(x,y)dy$

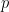
dengan $p(x,y) = \partial_xf = \partial f / \partial x|_{y}$ dan $q(x,y) = \partial_yf = \partial f/\partial y|_{x}$ . Jika peubah $x$ hendak diganti dengan peubah $p$ , maka diambil

$g(x,y) = f(x,y) - xp$

dengan diferensial total

$dg = df - pdx -xdp = -xdp +qdy$

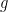
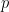
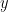
Untuk menghitung kegayutan $g$ secara eksplisit pada peubah $p$ dan $y$ saja, maka terlebih dahulu harus berlaku bahwa $p(x,y) = \partial_xf$ mempunyai invers untuk semua nilai $x$ . Selanjutnya, harga $x$ yang diperoleh disisipkan ke $g(x,y)$ untuk mendapatkan $g(p,y)$ .
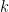
Perampatan yang lebih jauh juga dapat dilakukan. Diberikan fungsi diferensiabel $f(\lbrace x_i \rbrace) = f(x_1,...,x_k)$ dengan $k$ sembarang bilangan bulat positif.
maka dapat didefinisikan suatu fungsi baru

$g(\lbrace p_i \rbrace) = g(p_1,...,p_k) = f(\lbrace x_i \rbrace) - \sum_{i=1}^{k}(-x_ip_i)$

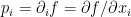
dengan $p_i = \partial_if = \partial f / \partial x_i$ .

Sumber : Greiner, W., Neise, L., Stoocker, H., (1995), Thermodynamics and Statisical Mechanics, Springer-Verlag, New York.

0 komentar:

Posting Komentar

Monggo komentar...

NARASOMA NOTEBOOK

Alihragam Legendre

0 komentar:

Posting Komentar

FACEBOOK SAYA

ARSIP SAYA

Manthiqut Thair

Entri Populer

LAMAN TERKAIT

CATATAN SAYA

Tamu dari Alam Lain

REKAN - REKAN