NARASOMA NOTEBOOK: Menghitung Volume Bola Berdimensi N dengan Jari

Menghitung Volume Bola Berdimensi N dengan Jari - Jari R

0 komentar
Posted in Label: Lintas Ilmu, Matematika untuk Fisika

Volume yang dimaksud, $V_N(R)$ mempunyai bentuk integral lipat

$V_N(R) = \int_{\sum_{i=1}^{N}x^2 \leqslant R^2}dx_1...dx_N = R^N \int_{\sum_{i=1}^{N}y^2 \leqslant 1}dy_1...dy_N$

dengan penyulihan 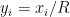$y_i = x_i/R$ . Kita dapat menulis

$V_N(R) = R^NC_N$ . . . (1)

dengan

$C_N = \int_{\sum_{i=1}^{3N}y^2 \leqslant 1}dy_1...dy_N$

Tampak bahwa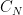 $C_N$ merupakan bola satuan berdimensi 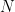$N$ . Untuk menghitung 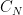$C_N$ , akan digunakan fakta

$\int_{-\infty}^{+\infty} \exp (-x^2)dx = \pi^{1/2}$

Oleh karena itu

$\int_{-\infty}^{+\infty}...\int_{-\infty}^{+\infty} \exp (-(x_1^2+...+x_N^2))dx_1...dx_N = \pi^{N/2}$

... (2)
Selanjutnya dilakukan aliharagam koordinat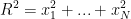 $R^2=x_1^2+...+x_N^2$ , dan elemen volume 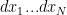$dx_1...dx_N$ diganti dengan elemen volume berbentuk cangkang (kulit) bola $dV_N(R)|_{ckg}$ , yakni

$dx_1...dx_N|_{ckg} = dV_N(R)|_{ckg} = NR^{N-1}C_NdR$

menurut persamaan (1). Maka persamaan (2) memberikan

$NC_N \int_0^{\infty} R^{N-1} \exp(-R^2)dR = \pi^{N/2}$ ... (3)

Jika disulihkan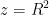 $z = R^2$ , maka persamaan (3) menjadi

$\frac{NC_N}{2}\int_0^{\infty} z^{\frac{N}{2}-1} \exp(-z)dz = \pi^{N/2}$

Ingat kembali fungsi Gamma $\Gamma(n)$ ,

$\Gamma(n) = \int_0^\infty z^{n-1}\exp(-z)dz$

Sehingga diperoleh

$\frac{NC_N}{2} \Gamma(\frac{N}{2}) = \pi^{N/2}$

atau

$C_N = \frac{\pi^{N/2}}{\frac{N}{2} \Gamma(\frac{N}{2})}$

Maka, volume bola yang kita cari adalah

$V_N(R) = \frac{R^N \pi^{N/2}}{\frac{N}{2} \Gamma(\frac{N}{2})}$

-------------------------------------------------------------------------------
Sebagai contoh, untuk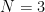 $N = 3$ dan dengan menggunakan rekursi fungsi Gamma $\Gamma(n+1) = n \Gamma(n)$ serta nilai $\Gamma(\frac{1}{2}) = \sqrt{\pi}$ , kita mendapatkan

$V_3(R) = \frac{R^3 \pi^{3/2}}{\frac{3}{2} \Gamma(\frac{3}{2})} = \frac{4}{3} \pi R^3$

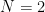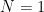Contoh lain, menggunakan cara serupa, untuk $N = 2$ dan $N = 1$ , kita dapatkan

$V_2(R) = \frac{R^2 \pi^{2/2}}{\frac{2}{2} \Gamma(\frac{2}{2})} = \frac{R^2 \pi}{1.0!}= \pi R^2$

dan

$V_1(R) = \frac{R^1 \pi^{1/2}}{\frac{1}{2} \Gamma(\frac{1}{2})} = 2R$

NB : Volume bola berdimensi dua dan satu dengan jari - jari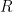 $R$ , masing - masing adalah luas cakram dengan jari - jari 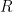$R$ dan panjang garis dari 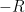$-R$ sampai 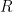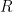$R$ ( $R$ satuan diukur dari sembarang titik acuan).

Sumber : Greiner, W., Neise, L., Stoocker, H., (1995), Thermodynamics and Statisical Mechanics, Springer-Verlag, New York.

0 komentar:

Posting Komentar

Monggo komentar...

NARASOMA NOTEBOOK

Menghitung Volume Bola Berdimensi N dengan Jari - Jari R

0 komentar:

Posting Komentar

FACEBOOK SAYA

ARSIP SAYA

Manthiqut Thair

Entri Populer

LAMAN TERKAIT

CATATAN SAYA

Tamu dari Alam Lain

REKAN - REKAN